lunes, 1 de junio de 2015
Números fraccionarios
Historia
Los Griegos tomaron elementos de
la matemática de los Babilonios y de
los Egipcios. La innovación más
importante fue la invención de las matemáticas
abstractas basadas en una estructura lógica de definiciones, axiomas y demostraciones. Según los cronistas griegos, este avance comenzó en el siglo
VI a.c. con Tales de Mileto y Pitágoras de Samos. Este último enseñó
la importancia del estudio de los números para poder entender el mundo. Algunos
de sus discípulos hicieron importantes descubrimientos sobre la teoría de
números y la geometría, que se atribuyen al propio Pitágoras.
Número
fraccionario
a
Los
números fraccionarios son aquellos números que se escriben de la forma ---- , donde llamaremos a Numerador
y b denominador. Por ejemplo: b
Significado de las fracciones
Las fracciones tienen diferentes significados: Como parte de un objeto, la fracción de un conjunto, la fracción como operador y la fracción como número decimal.
Fracción como parte de un objeto
Las fracciones se utilizan para representar las partes de un objeto cualquiera. Por ejemplo:
La fracción de un conjunto
La fracción como operador
Consideremos la fracción como una máquina que al operar sobre un número lo divide entre el denominador y luego lo multiplica por el numerador. Por ejemplo:
La fracción como número decimal
sábado, 30 de mayo de 2015
Clasificación de las fracciones
Las
fracciones se pueden clasificar en fracciones propias, fracciones impropias, homogéneas,
heterogéneas y fracciones equivalentes.
Son
aquellas fracciones en las cuales el numerador es menor
que el denominador, es decir
aquellas fracciones que son
menores que la unidad. Por ejemplo:
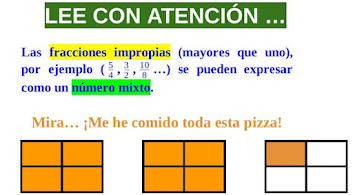
Son
aquellas fracciones en las cuales el numerador es mayor
que el denominador, es decir
aquellas fracciones que son
mayores que la unidad. Por ejemplo:
Si
representáramos las fracciones anteriores en la recta numérica, se puede observar que estas son mayores que la unidad. Por ejemplo:
Son
aquellas fracciones en las cuales el denominador es el mismo. Por ejemplo:
Son
aquellas fracciones en las cuales el denominador es diferente.
Por ejemplo:
Son
aquellas fracciones que representan una misma cantidad, es decir un mismo número.
Por ejemplo:
Veamos un video de fracciones equivalentes
Representación de las fracciones
Los
números fraccionarios se pueden representar
por medio de figuras, rectas o conjuntos, lo importante es tener en cuenta que todas las partes en que se divida la
unidad sean iguales. Por ejemplo:
Amplificación de las fracciones
Amplificar
una fracción equivale a multiplicar
el numerador y el denominador por un mismo número natural, para obtener una
fracción equivalente. Por ejemplo:
Simplificación de las fracciones
Simplificar
una fracción equivale a
dividir el numerador y el denominador por un mismo divisor común, para obtener una fracción equivalente. Por ejemplo:
viernes, 29 de mayo de 2015
Operaciones con los fraccionarios
Suma
y/o resta de fraccionarios
Para sumar y/o restar
fracciones se debe tener en cuenta si
las fracciones son homogéneas o heterogéneas.
Suma y/o
resta de fracciones homogéneas
Si
las fracciones son homogéneas, se
suman y/o restan los numeradores y se coloca el mismo denominador, luego se simplifica el resultado si es posible.
Por ejemplo:
Suma y/o
resta de fracciones heterogéneas
Si
las fracciones son heterogéneas primero se realizan las amplificaciones o simplificaciones adecuadas para que
las fracciones queden con el mismo
denominador (homogéneas) y finalmente se aplica el método anterior. Por
ejemplo:
Veamos un video de fracciones
jueves, 28 de mayo de 2015
Multiplicación de fraccionarios
Al multiplicar fraccionarios puede ocurrir
que se multipliquen un natural
por un fraccionario, una fracción
por una fracción.
Natural por
fraccionario
En esta multiplicación, se
multiplica el natural por el numerador de la fracción y se coloca el mismo
denominador, es decir:
Fracción por fracción
En esta
operación se multiplican los numeradores
entre sí y los denominadores entre sí, es decir:
En
la multiplicación de fraccionarios se cumplen las propiedades clausurativa, modulativa, conmutativa,
asociativa, uniforme y la invertiva
(inverso multiplicativo).
División de fraccionarios
Para dividir fraccionarios se debe identificar el dividendo y el divisor. La división es la operación inversa a la multiplicación, por lo tanto para dividir un fraccionario por otro fraccionario, se multiplica el dividendo por el inverso multiplicativo del divisor, es decir:
miércoles, 27 de mayo de 2015
Ecuaciones y problemas en los fraccionarios
Ecuaciones
en los fraccionarios
Hay ecuaciones en las que aparecen, además de sumas y de
restas, multiplicaciones y divisiones
acompañando la variable. Si en una ecuación tenemos una cantidad que multiplica la variable y la
cambiamos de lado, entonces la cantidad pasa al otro lado de la ecuación a dividir, es decir:
Si en una ecuación tenemos una cantidad que divide la variable y la
cambiamos de lado, entonces la cantidad pasa al otro lado de la ecuación a multiplicar, es decir:
Para resolver ecuaciones en los fraccionarios se hace un procedimiento, aplicando:
1) Se despeja la variable, es decir que se busca dejarla sola
2) Se aplican las propiedades de la suma (resta), multiplicación (división).
3) Sí un entero está sumando, pasa al otro lado de la igualdad a restar o viceversa.
4) Sí un entero está multiplicando, pasa al otro lado de la igualdad a dividir o viceversa.
5) Se hace la prueba para verificar que se cumple una igualdad.
Por ejemplo
Problemas de aplicación
Para
resolver problemas en los fraccionarios, primero se
debe identificar la cantidad
desconocida y luego formar una ecuación.
Por
ejemplo
1) Dos tercios de los habitantes de un
pueblo saben leer y escribir. Tres cuartos de las personas que saben
leer y escribir son profesionales. ¿Qué
fracción de los habitantes son profesionales? ¿Qué fracción de la
población no sabe leer y escribir?
2) Una
cinta se fracciona en 5 partes iguales.
Sí la cinta mide siete décimos de metro,
¿Qué fracción representa a cada pedazo?
Aprovechando todas las herramientas que
nos traen las TIC, y los recursos didácticos en el proceso ENSEÑANZA
APRENDIZAJE de la matemática, en las siguientes direcciones electrónicas
podemos encontrar lecturas complementarias y una serie de animaciones que nos
ayudarán a una mejor comprensión de todo lo relacionando con los números
fraccionarios y su aplicabilidad en la naturaleza.
Lógica y conjuntos
Los números naturales
Potencias, radicales y logaritmos en los naturales
Suscribirse a:
Entradas (Atom)